04.07.2024

Eine alternative Geschichte der Quantitativen Spektroskopie

Dr. Thomas G. Mayerhöfer , Dr. Susanne Pahlow, Prof. Jürgen Popp, Leibniz-Institut für Photonische Technologien (IPHT)

Die Geschichte der quantitativen Spektroskopie begann im 18. Jahrhundert mit den grundlegenden Arbeiten von Pierre Bouguer und Johann Heinrich Lambert, die wesentliche Beiträge zum Verständnis der Lichtabsorption leisteten. Bouguer, ein französischer Physiker, veröffentlichte 1729 sein Werk "Essai d'Optique", in dem er die Abschwächung des Lichtes beim Durchgang durch ein Medium beschrieb.[1] Diese Arbeit bildete die Grundlage für das später als Bouguer-Lambert-Gesetz bekannte Prinzip.

Johann Heinrich Lambert, ein deutscher Mathematiker und Physiker, erweiterte Bouguers Forschung und formulierte 1760 das Gesetz der Absorption in "Photometria".[2] Das Bouguer-Lambert-Gesetz beschreibt die logarithmische Abschwächung der Lichtintensität in Abhängigkeit von der Strecke, die das Licht durch ein absorbierendes Medium zurücklegt.

1857 veröffentlichten Robert Bunsen und Henry Roscoe eine Arbeit, in der sie die logarithmische Abschwächung nachwiesen, wobei sie explizit die Reflexion an der Vorder- und Rückseite des Probenbehälters einbezogen.[3] In ihrer Arbeit führten sie den Extinktionskoeffizienten ein, und ihre Formel kam der modernen Form des Lambert-Beer-Gesetzes bereits ziemlich nahe.

Ein wenig früher untersuchte August Beer, wie sich Küvettendicke, Farbstoffkonzentration und Transmission zueinander verhalten, und fand heraus, dass gleiche Produkte aus Dicke und Konzentration zu gleichen Transmissionen führten.[4] Beers Arbeit aus dem Jahr 1852 ist heute ein Grundprinzip in der quantitativen Analyse mittels Spektroskopie. Kombiniert man seine Entdeckung mit der Form des Absorptionsgesetzes von Bunsen und Roscoe, indem man den Extinktionskoeffizienten als Produkt von Konzentration und molarem Extinktionskoeffizienten betrachtet, resultiert daraus das Lambert-Beer-Gesetz.

Diese Form wurde jedoch erst nach 1905 vorherrschend (sie ist noch nicht in Kaysers Handbuch der Spektroskopie zu finden,[5] obwohl Kayser ausdrücklich erwähnt, dass der Extinktionskoeffizient proportional zur Konzentration ist), und es ist nicht ganz klar, wer es in dieser Form zuerst verwendete - wahrscheinlich waren es Luther und Nikolopulos im Jahr 1913.[6] Es ist erwähnenswert, dass sowohl Beer als auch Kayser genau wie Bunsen und Roscoe grundsätzlich die Reflexion an den Grenzflächen einbezogen, basierend auf den Fresnelschen Gesetzen von 1831.[7] Im Gegensatz dazu werden diese Reflexionen heute nicht mehr berücksichtigt. Der Grund ist, dass man implizit annimmt, dass der Bezug auf eine Referenzmessung den Einfluss der Reflexion herausrechnen kann, was bei der Spektrophotometrie relativ gut funktioniert. In anderen Systemen, wie einer reinen Flüssigkeit oder einer Schicht auf einem Substrat, ist diese Methode jedoch nicht anwendbar.

Ein weiteres Problem stellt die Konzentration dar. August Beer wies bereits in seiner Arbeit darauf hin, dass die von ihm gefundene Proportionalität nur für niedrige Konzentrationen gilt und man vorsichtig sein sollte, sein Gesetz auf höhere Konzentrationen auszudehnen. Dies scheint logisch, da höhere Konzentrationen mit größerer Wahrscheinlichkeit zu Wechselwirkungen zwischen den Farbstoffmolekülen führen. Dies ist in der Tat korrekt, jedoch in einer völlig anderen Form als heute allgemein angenommen. Wir werden darauf zurückkommen, wenn wir den Beitrag von Hendrik Antoon Lorentz besprechen.

An dieser Stelle muss betont werden, dass dies im Wesentlichen der Stand der Theorie in der quantitativen Spektroskopie ist. Zudem weiß man seit der Einführung der Quantenmechanik, dass Spektren quantenmechanische Übergänge widerspiegeln. Das alle Materie als ideales Gas behandelt wird, führt jedoch zu der irrigen Annahme, dass die Lage eines Maximums in einem Absorptionsspektrum dem Unterschied zwischen dem Grund- und dem angeregten Zustand entspricht. Tatsächlich ist dies aus verschiedenen Gründen nicht der Fall, die erst verständlich werden, wenn man einbezieht wie kondensierte Materie von Licht polarisiert wird und das Licht als elektromagnetische Welle beschrieben werden kann.

Interessanterweise hat man keine Probleme, Materie Welleneigenschaften zuzuordnen, obwohl dieses Ergebnis der Quantenmechanik nicht intuitiv ist. Was Licht betrifft, impliziert die Lambert-Beer-Approximation jedoch, dass ihm Welleneigenschaften fehlen, da es die Änderungen von Intensitäten statt Änderungen von elektromagnetischen Feldern beschreibt. Dies ist konsequent, da die elektromagnetische Theorie erst nach den bislang beschriebenen Arbeiten erarbeitet wurde.

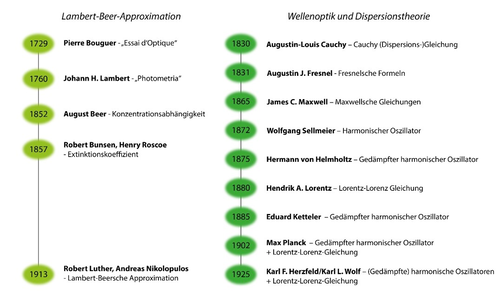
Abb.1: Meilensteine der quantitativen Spektroskopie

Mit der Beschreibung der elektromagnetischen Phänomene durch James Clerk Maxwell in den 1860er Jahren wurde ein besseres Verständnis der Lichtnatur erreicht.[8] Maxwells Theorien verbanden Elektrizität und Magnetismus und beschrieben Licht als elektromagnetische Welle. Diese Theorie erweiterte die Möglichkeiten der Spektroskopie auf das gesamte elektromagnetische Spektrum. Nach Maxwells Wellentheorie ist die dielektrische Funktion die Materialeigenschaft, während der komplexe Brechungsindex eigentlich eine Welleneigenschaft ist. Damit Maxwells Gleichungen Lösungen haben, müssen sie durch Materialgleichungen ergänzt werden. Daher benötigt man eine Dispersionstheorie.

In den Jahren unmittelbar nach Maxwells Arbeit, basierten Dispersionstheorien immer noch auf der Annahme von Ätherwellen, was die Anwendbarkeit der Ergebnisse jedoch nicht beeinträchtigte. Der erste, der eine gute Beschreibung der Dispersion des Brechungsindex auf der Grundlage der Annahme eines harmonischen Oszillators erreichte, zumindest in den Bereichen normaler Dispersion, war Wolfgang Sellmeier.[9] Hierzu ist jedoch eine Bemerkung angebracht. Im vorherigen Absatz wurde erwähnt, dass der Brechungsindex keine Materialgröße ist - jetzt scheint es jedoch, dass er direkt mit Materialeigenschaften korreliert werden kann. Tatsächlich beschreiben Dispersionstheorien nicht die Dispersion des Brechungsindex, sondern seines Quadrates, also der dielektrischen Funktion. Dieser einfache Zusammenhang gilt auch nur für isotrope und skalare Materialien; für anisotrope Materialien wird die dielektrische Funktion zum Tensor.

Zurück zur Beschreibung der Dispersion mit Hilfe eines Oszillatormodells. Nach Sellmeier kamen Hermann von Helmholtz und Eduard Ketteler auf die Idee, den gedämpften harmonischen Oszillator einzuführen, was zu einem Modell führte, das nun auch anomale Dispersion und Absorption richtig beschreiben konnte (obwohl nur Kettelers Modell auch eine akkurate Beschreibung über den gesamten Spektralbereich lieferte).[10,11] Damit war die Grundlage geschaffen, Spektren mittels Wellenoptik und Dispersionstheorie zu beschreiben. Es fehlte jedoch noch ein wichtiges Puzzlestück, das von Hendrik Antoon Lorentz geliefert wurde.

Lorentz stellte sich die Frage, inwiefern der Brechungsindex von der sogenannten Körperdichte abhängig sein könnte.[12] Wenn wir von einem Gas ausgehen und das Volumen verringern, so erhöht sich die (molare) Konzentration seiner Moleküle - eine einfache Beschreibung liefert das ideale Gasgesetz und damit seine Dichte. Tatsächlich beobachtet man anfangs ein lineares Anwachsen des Brechungsindex mit der Dichte, stellt aber fest, dass er bei höheren Drücken und beim Übergang in eine kondensierte Phase überproportional anwächst. Die Erklärung ist relativ einfach. Bei niedrigen Drücken haben die Gasmoleküle große mittlere Abstände. Strahlt man Licht ein, so wird das Molekül polarisiert. Diese Polarisation beeinflusst jedoch keine benachbarten Moleküle, solange die Abstände relativ groß sind, d.h. die Polarisation ist proportional zum eingestrahlten elektrischen Feld.

Verringert man die Abstände, so fangen die Moleküle unter Lichteinwirkung an, sich gegenseitig zu beeinflussen, wodurch sich nichtlineare Anteile ergeben (diese Nichtlinearität sollte nicht mit der verwechselt werden, die sich durch sehr starke Lichtquellen ergibt). Letztendlich lässt sich dieser Effekt so beschreiben, dass man zu dem eingestrahlten Feld noch ein zusätzliches erhält, welches die wechselseitige Beeinflussung beschreibt. Insgesamt ist also das am Ort eines Moleküls wirksame elektrische Feld größer als das eingestrahlte.

Noch eine kleine Bemerkung zum Zusammenhang zwischen Brechungsindex und Dichte. Basierend auf den Arbeiten von Landolt an homologen Verbindungen (aufgenommen nicht zuletzt auf einen Ratschlag von August Beer) hätte man auf die Idee kommen können, dass es nicht die Dichte ist, zu der der Brechungsindex proportional ist, sondern die molare Konzentration der farbgebenden Gruppe.[13,14] Für organische Kohlenwasserstoffe ist dies beispielsweise die C-H Bindung, deren Absorption im fernen UV liegt. Tatsächlich wurde dieser Zusammenhang aber erst vor kurzem entdeckt.[15]

Lorentz mag anfangs nur den reellen Brechungsindex im Sinn gehabt haben. Anfang des 20. Jahrhunderts beschäftigte sich jedoch ein anderer Nobelpreisträger mit der Dispersionstheorie und berücksichtigte dabei auch das durch Polarisation von Materie vergrößerte elektrische Feld am Ort des Moleküls. Ketteler hatte bereits beschrieben, dass das Maximum des Absorptionsindexes (das Gleiche gilt für die Absorbanz, denn diese ergibt sich als Produkt der Wellenzahl und des Absorptionsindexes mal einer Konstante) nicht der Eigenfrequenz des Oszillators entspricht oder, gemäß der Terminologie der Quantenmechanik, dem energetischen Abstand von Grund- und angeregtem Zustand, sondern blauverschoben ist. Aufgrund des lokalen Feldes trat nun eine Rotverschiebung auf, die umso stärker ist, je größer die Oszillatorstärke (diese entspricht dem Produkt aus Übergangsmoment und molarer Konzentration des Oszillators) ist.

Damit hatte Max Planck explizit nachgewiesen, dass das Beersche Gesetz eine Näherung ist, die umso besser wird, je schwächer das Übergangsmoment ist. D.h. das Beersche Gesetz ist nur für den Fall verschwindender Absorption streng gültig.[16,17] Wen die entsprechenden Überlegungen noch nicht überzeugen, der sei darauf hingewiesen, dass beispielsweise Edelgase nur aufgrund des beschriebenen Mechanismus flüssig oder fest werden - dazu wird keine Lichteinstrahlung benötigt.[18] Stattdessen reichen dazu Vakuumfluktuationen aus.

Interessanterweise überlegte Planck auch, wie die Rotverschiebung des Absorptionspeaks experimentell nachgewiesen werden könnte. Was er explizit ausschloss, waren optische Konfigurationen, bei denen sich "stehende Wellen" bilden könnten, da es auch dabei zu Peakverschiebungen oder Farbänderungen kommen könnte. Was haben stehende Wellen mit Farben zu tun? Nach einem Regenguss lässt sich in manchen Pfützen ein Farbeffekt beobachten, der durch dünne Öl- oder Benzinfilme zustande kommt. Dabei interferieren Lichtwellen miteinander, die sich in gegensätzlicher Richtung durch die Filme bewegen. Bei destruktiver Interferenz werden bestimmte Frequenzen ausgelöscht, wohingegen andere durch konstruktive Interferenz verstärkt werden. Als Konsequenz entsteht Farbe, obwohl keine Absorption vorliegt. Allerdings können Absorptionen durch Interferenz verstärkt oder abgeschwächt und die Peakpositionen maßgeblich verschoben werden. Das war Planck offensichtlich bewusst, wohingegen dieser Effekt vielen Spektroskopikern heutzutage unbekannt ist. Warum? Vielleicht weil Interferenz eine Welleneigenschaft ist und die Benutzung der Lambert-Beer-Approximation dem Licht Welleneigenschaften abspricht. Wir kommen später nochmal darauf zurück.

Planck benutzte nur einen Oszillator in seiner Dispersionstheorie. Das ist nicht realistisch, aber um die wesentlichen Aspekte seiner Theorie zu untersuchen, schien das ausreichend zu sein. Tatsächlich tritt ab dem Vorhandensein eines weiteren Oszillators ein interessanter Effekt auf, der darin besteht, dass nun das lokale elektrische Feld nicht nur zu einer Rotverschiebung des spektralen Peaks führt. Stattdessen sind nicht nur alle Peakpositionen gekoppelt, sondern zusätzlich auch die Oszillatorstärken bzw. die Bandenflächen, und zwar vom Röntgenbereich über das UV, den sichtbaren Bereich, das IR bis hin zum Mikrowellenbereich.[19,20] Mit anderen Worten: Weder die Intensität noch die Fläche einer Bande sind im Allgemeinen proportional zur molaren Konzentration, und Peakpositionen können nicht direkt als Abstand zwischen Grund- und angeregtem Zustand interpretiert werden.

Dieser Effekt spielt auch eine wichtige Rolle in der Solvatochromie. Bevor ein Spektrum oder eine Reihe von Spektren quantitativ evaluiert werden kann, müssen erst diese Effekte korrigiert werden. Die gute Nachricht ist, dass sich diese Effekte oft bei schwächeren Banden vernachlässigen lassen. Auch ist es generell nicht notwendig, bei Darstellungen der Absorbanz als Funktion der molaren Konzentration unbedingt eine Gerade anzufitten - der Zusammenhang zwischen Absorbanz und Konzentration ermöglicht analytische Anwendungen durchaus auch wenn er nichtlinear ist -, solange die Steigung der Kurve sich nicht an Null annähert.

Natürlich spricht nichts dagegen, eine bestimmte Näherung zu benutzen, allerdings sollte man sich immer im Klaren darüber sein, was man vernachlässigt. Eine weitere Annahme der Lambert-Beer-Approximation ist, dass ein Medium homogen ist. Für ein Gas oder eine Gasmischung stellt sich dieses Problem nicht, insbesondere wenn man Gase als ideal annimmt. Wenn man von Phasentrennung in Flüssigkeiten absieht, kann man eine flüssige Mischung als mikro-homogen annehmen, was impliziert, dass die Mischung für alle Wellenlängen eines bestimmten Wellenlängenbereichs auch unter dem Mikroskop als homogen erscheint. Feste Proben sind allerdings häufig mikro-heterogen. Was hat das für Konsequenzen?

Natürlich kann Streuung auftreten, was zu sehr komplexen Spektren führen kann, die nicht mehr ohne weiteres ausgewertet werden können. Oft wird in diesem Zusammenhang von Artefakten durch Mie-Streuung gesprochen. Gustav Mie behandelte in seiner Theorie jedoch nur Kugeln.[21] Zwar lässt sich seine Theorie auch auf nicht-sphärische Körper ausdehnen, in der spektroskopischen Praxis hat man es jedoch meistens nicht mit Teilchen zu tun, die weit voneinander separiert sind. Dadurch kommt es zu Mehrfachstreuung, was dazu führt, dass es keine analytische Möglichkeit mehr gibt, Spektren zu korrigieren. Falls die Teilchen sehr kleine Abstände aufweisen, wie beispielsweise in gepressten oder sogar zusammen gesinterten Pulvern, ist Streuung meistens kein Problem mehr. Stattdessen tritt dann bei mikro-heterogenen Proben ein Effekt auf, der weitgehend unbekannt ist.

Eine Ausnahme stellt eine Arbeit von R. Norman Jones aus dem Jahr 1952 dar.[22] Jones beschäftigte sich mit der sogenannten KBr-Methode, bei der pulverförmige Proben in einem sehr großen Überschuss von transparentem Material eingebettet werden, das die Fähigkeit hat, unter Druck zu fließen. Bei Druckanwendung entstehen Tabletten, die dann in Transmission gemessen werden. Falls das spektroskopische Material homogen verteilt ist, lässt sich die Lambert-Beer-Approximation anwenden, aber die Peakpositionen stärkerer Banden werden wiederum durch den Effekt lokaler Felder verschoben. Manchmal kommt es jedoch dazu, dass sich das Probenmaterial zwischen den entstehenden Kristalliten des Matrixmaterials ansammelt. Dann entstehen Bereiche, die stark absorbierend sind und in nicht absorbierendem Material eingebettet sind. Sind diese Bereiche nicht klein im Vergleich zur Wellenlänge, so wird ein Teil des Lichts hindurchgehen, ohne mit den Absorbern in Berührung gekommen zu sein.

Jones zeigte, dass dies zu einem Abflachen der Absorbanz-Konzentrationskurven führt. Wer Schwierigkeiten hat, sich diesen Effekt vorzustellen, sollte an einen Mikrowellenherd denken. In diesem befindet sich ein Metallgitter hinter dem Glas. Die Abstände zwischen dem Metall sind groß relativ zur Wellenlänge des sichtbaren Lichts, sodass man bequem hindurchschauen kann. Für die Mikrowellen erscheinen das Gitter und die Löcher dazwischen als homogenes Medium, weshalb die Mikrowellen absorbiert werden.

Man kann sich das Ganze auch idealisiert als Probe mit schachbrettartiger Struktur vorstellen, bei der die schwarzen Felder absorbierend sind, während die weißen Felder kein Licht absorbieren. Das Verhältnis der Fläche und des Volumens der schwarzen zu den weißen Feldern ist immer 1:1. Deshalb sollten die Spektren einer solchen idealisierten Probe gemäß der Lambert-Beer-Approximation nicht von der Kantenlänge der Felder abhängig sein.

Leider hat das Problem in der Wellenoptik keine analytische Lösung, aber numerische Verfahren können verwendet werden, um die Maxwellschen Gleichungen an verschiedenen Gitterpunkten innerhalb der fiktiven Probe zu lösen und damit die Transmission durch das Schachbrett hindurch zu berechnen. Es stellt sich heraus, dass die Spektren stark von der Seitenlänge der Quadrate abhängen, wenn diese Seitenlänge im Bereich der Lichtwellenlänge liegt. Für sehr kleine Seitenlängen nähert sich das Ergebnis dem der Lorentz-Lorenz-Theorie an. Für große Seitenlängen findet man, dass man die Transmissionsspektren berechnen kann, indem man über die Transmissionsspektren der schwarzen und weißen Felder mittelt, d.h. in Wirklichkeit sind nicht die Absorbanzen additiv, sondern die Transmittanz und die Reflektanz. Für einen Spektroskopiker ist dieses Ergebnis befremdlich, denn in den Lehrbüchern der Spektroskopie ist es die Absorbanz, die additiv ist. Dieser scheinbare Widerspruch entsteht dadurch, dass die (näherungsweise) Additivität der Absorbanz voraussetzt, dass eine Mischung mikro-homogen ist.[23]

Bis hierhin haben wir strenggenommen nur skalare Materialien betrachtet, d.h. einkomponentige Systeme, die eine kubische Kristallstruktur aufweisen oder zufällig orientierte Materialien, bei denen die Kristallite oder geordneten Bereiche mikro-homogen sind. Für anisotrope Proben hat sich in der Spektroskopie eine Theorie etabliert, die oft als Lineardichroismus-Theorie bezeichnet wird. Diese wurde wahrscheinlich von Rudolf Zbinden 1964 eingeführt und stellt eine Erweiterung der Lambert-Beer-Approximation dar.[24] Dementsprechend hängt die Absorbanz nur vom Winkel zwischen Übergangsmoment und Polarisationsrichtung ab.

Auch dieses Konzept setzt ein ideales Gas voraus. Dies klingt zunächst paradox, da es in Gasen keine Vorzugsrichtung geben kann. Das eigentliche Problem ist jedoch, dass die Lineardichroismus-Theorie die Existenz von Grenzflächen nicht berücksichtigt. Gemäß einer der Maxwellschen Gleichungen ergibt sich, dass nur die tangentiale Komponente des elektrischen Feldes an Grenzflächen kontinuierlich ist. Dies führt dazu, dass es nicht nur auf den Winkel zwischen Übergangsmoment und Polarisationsrichtung ankommt, sondern auch auf den Winkel zwischen Übergangsmoment und Grenzfläche. In Zbindens Betrachtungen wird dies nicht erwähnt (und auch in keiner Abhandlung, die davon abgeleitet ist). Trotzdem handelt es sich auch hier nicht um eine neuere Erkenntnis.

Paul Drude beschäftigte sich bereits in seiner Doktorarbeit (erschienen 1887!) damit, Gleichungen aufzustellen, mit denen man die Reflektanz und Transmittanz von Kristallen bis hin zur triklinen Kristallsymmetrie berechnen konnte.[25] Diese rein theoretische Arbeit wurde dann von Frank Matossi und Florenz Dane 1927 experimentell verifiziert.[26] Diese Arbeit wies auch explizit die Bedeutung des Winkels zwischen Grenzfläche und Übergangsmoment nach: Je größer dieser Winkel, desto mehr wird der Peak der zugehörigen Bande ins Blaue verschoben. Dementsprechend lassen sich Orientierungen viel genauer bestimmen, als dies auf Basis der Lineardichroismus-Theorie möglich gewesen wäre.

Dies ist ein Aspekt, der nicht genug betont werden kann: Die Lambert-Beer-Approximation und ihre Erweiterung für anisotrope Proben führen dazu, dass wir Spektroskopiker in unserem Denken eingeengt werden und viele Möglichkeiten nicht sehen, die sich uns bieten. So wie es möglich ist, die Orientierung viel genauer als gedacht zu bestimmen, so eröffnet uns die Spektroskopie auch durch die Wellennatur des Lichts die Möglichkeit, morphologische Unterschiede aufzuspüren.

Ein weiteres Beispiel, das wir noch nicht erwähnt haben, basiert auf dem von Lorentz beschriebenen Effekt. Die Lorentz-Lorenz-Theorie gilt nämlich nur für kugelförmige Moleküle in Umgebungen mit sphärischer Symmetrie. Mischt man beispielsweise Benzol und Toluol und versucht, die Spektren der Mischung mit der Lorentz-Lorenz-Theorie zu simulieren, stellt man fest, dass die Bandenverschiebungen größer sind, als sie nach Lorentz-Lorenz sein dürften.

Dass die Lorentz-Lorenz-Theorie nicht der Weisheit letzter Schluss ist, war bereits zu Beginn des 20. Jahrhunderts bekannt, weshalb Erweiterungen wie die Maxwell-Garnett-Theorie (1904),[27,28] die Bruggeman-Effektive-Medien-Theorie (1935),[29] und schließlich die Bergmann-Darstellung[30] entwickelt wurden. Letztere lässt sich zeigen, dass sie alle anderen Theorien umfasst.

Trotzdem kann auch sie nicht solche starken Bandenverschiebungen vorhersagen, wie sie im System Benzol-Toluol auftreten. Dies liegt wahrscheinlich daran, dass sowohl Benzol als auch Toluol keine kugelförmigen Moleküle sind und dass die Umgebung der einzelnen Moleküle sicherlich auch keine kugelförmige Symmetrie aufweist. Daraus lässt sich schließen, dass Licht auch empfindlich für die Form und die Umgebung von Molekülen ist, selbst wenn diese viel kleiner als die Lichtwellenlänge sind, wie z.B. im infraroten Spektralbereich.

All diese und noch mehr Beispiele sind dem neu erschienenen Buch "Wave Optics in Infrared Spectroscopy - Theory, Simulation and Modelling" entnommen.[23] Das Ziel dieses Buches ist es, den spektroskopisch vorgebildeten Leser auf das Niveau der Wellenoptik und Dispersionstheorie zu bringen. Das Buch ist in zwei Abschnitte unterteilt, wobei sich der erste Abschnitt mit skalaren Theorien befasst (siehe Abbildung 2), während der zweite Abschnitt anisotrope Materialien und deren optische Eigenschaften behandelt.

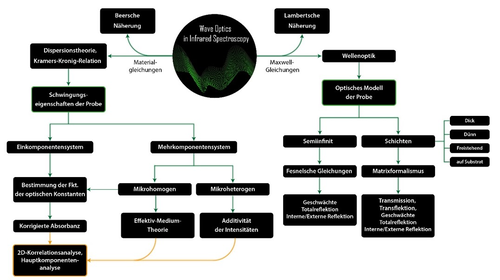
Abb.2: Wichtige Teilaspekte und Gebiete der quantitativen Spektroskopie.[23]

Wir hoffen, dass die vorgestellten Überlegungen und Beispiele den interessierten Leser dazu motivieren können, tiefer in die Theorie der Spektroskopie einzutauchen und sich damit fortgeschrittene Anwendungsmöglichkeiten zu erschließen, insbesondere mit den enormen apparativen Fortschritten, die in den letzten Jahren gemacht worden sind.

Danksagung

Wir bedanken uns für finanzielle Unterstützung von der EU, dem "Thüringer Ministerium für Wirtschaft, Wissenschaft und Digitale Gesellschaft", der "Thüringer Aufbaubank", dem Bundesministerium für Bildung und Forschung, Deutschland (BMBF), der Deutschen Forschungsgemeinschaft, dem "Fonds der Chemischen Industrie" und der Carl-Zeiss-Stiftung.

Referenzen

1. P. Bouguer. Essai d'Optique. 1729.
   
2. J.H. Lambert, E. Anding. Lambert's photometrie: (photometria sive de mensura et gradibus luminis, colorum et umbrae). (1760). Heft 3, Tl. 6 und 7 - Anmerkungen. Engelmann, 1892.
   
3. R. Bunsen, H. Roscoe. "IV. Photochemische Untersuchungen". Poggendorffs Annalen. 1857. 101: 235-263.
   
4. Beer. "Bestimmung der Absorption des rothen Lichts in farbigen Flüssigkeiten". Annalen der Physik. 1852. 162(5): 78-88.
   
5. H. Kayser. Handbuch der Spektroskopie, Vol. 3. Verlag von S. Hirzel, 1905.
   
6. R. Luther, A. Nikolopulos. "Über die Beziehungen zwischen den Absorptionsspektren und der Konstitution der komplexen Kobaltamminsalze". Z. Phys. Chem. 1913. 82U(1): 361.
   
7. A. Fresnel. "Ueber das Gesetz der Modificationen, welche die Reflexion dem polarisirten Lichte einprägt". Annalen der Physik. 1831. 98(5): 90-126.
   
8. J.C. Maxwell. "VIII. A dynamical theory of the electromagnetic field". Philosophical Transactions of the Royal Society of London. 1865. 155: 459-512.
   
9. W. Sellmeier. "Ueber die durch die Aetherschwingungen erregten Mitschwingungen der Körpertheilchen und deren Rückwirkung auf die ersteren, besonders zur Erklärung der Dispersion und ihrer Anomalien". Annalen der Physik. 1872. 223(11): 386-403.
   
10. H. Helmholtz. "Zur Theorie der anomalen Dispersion". Annalen der Physik. 1875. 230(4): 582-596.
    
11. E. Ketteler. Theoretische Optik: gegründet auf das Bessel-Sellmeier'sche Princip. Zugleich mit den experimentellen Belegen. F. Vieweg, 1885.
    
12. H.A. Lorentz. "Ueber die Beziehung zwischen der Fortpflanzungsgeschwindigkeit des Lichtes und der Körperdichte". Annalen der Physik. 1880. 245(4): 641-665.
    
13. H. Landolt. "Ueber die Brechungsexponenten flüssiger homologer Verbindungen". Annalen der Physik. 1862. 193(11): 353-385.
    
14. H. Landolt. "Ueber den Einfluss der atomistischen Zusammensetzung C, H und O-haltiger flüssiger Verbindungen auf die Fortpflanzung des Lichtes". Annalen der Physik. 1864. 199(12): 595-628.
    
15. T.G. Mayerhöfer, S. Spange. "Understanding Refractive Index Changes in Homologous Series of Unbranched Organic Compounds Based on Beer's Law". Chemphyschem. 2023. 24(19): e202300430.
    
16. M. Planck. "Zur elektromagnetischen Theorie der Dispersion in isotropen Nichtleitern". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften. 1902. I: 470-494.
    
17. M. Planck. "Zur elektromagnetischen Theorie der selectiven Absorption in isotropen Nichtleitern". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften. 1903. I: 480-498.
    
18. F. London. "Zur Theorie und Systematik der Molekularkräfte". Zeitschrift für Physik. 1930. 63(3): 245-279.
    
19. K.F. Herzfeld, K.L. Wolf. "Die Dispersion von Kaliumchlorid und Natriumchlorid". Annalen der Physik. 1925. 383(17): 35-56.
    
20. O. Fuchs, K.L. Wolf. "Reststrahlfrequenzen, Eigenfrequenzen und Dispersion im Ultraroten". Zeitschrift für Physik. 1928. 46(7-8): 506-518.
    
21. G. Mie. "Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen". Annalen der Physik. 1908. 330(3): 377-445.
    
22. R.N. Jones. "The Absorption of Radiation by Inhomogeneously Dispersed Systems". Journal of the American Chemical Society. 1952. 74(10): 2681-2683.
    
23. T.G. Mayerhöfer. Wave Optics in Infrared Spectroscopy - Theory, Simulation and Modeling. Philadelphia: Elsevier, 2024.
    
24. R. Zbinden. Infrared spectroscopy of high polymers. New York-London: Academic Press, 1964.
    
25. P. Drude. "Ueber die Gesetze der Reflexion und Brechung des Lichtes an der Grenze absorbirender Krystalle". Annalen der Physik. 1887. 268(12): 584-625.
    
26. F. Matossi, F. Dane. "Reflexion, Dispersion und Absorption von Kalkspat im Absorptionsgebiet bei 7 μ". Zeitschrift für Physik. 1927. 45(7): 501-507.
    
27. J.C.M. Garnett, J. Larmor. "XII. Colours in metal glasses and in metallic films". Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character. 1904. 203(359-371): 385-420.
    
28. J.C.M. Garnett, J. Larmor. "VII. Colours in metal glasses, in metallic films, and in metallic solutions.-II". Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character. 1906. 205(387-401): 237-288.
    
29. D.A.G. Bruggeman. "Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen". Annalen der Physik. 1935. 416(7): 636-664.
    
30. D.J. Bergman. "The dielectric constant of a composite material-A problem in classical physics". Physics Reports. 1978. 43(9): 377-407.

» Artikel als pdf (374 KByte)