01.02.2024
![]()
Solvatochromie im Wandel der Zeit - was sich aus der Vergangenheit für die Zukunft lernen lässt
Dr. Thomas G. Mayerhöfer , Leibniz-Institut für Photonische Technologien (IPHT)
Dr. Stefan Spange, Technische Universität Chemnitz
Solvatochromie ist ein faszinierendes Phänomen, das auf der beeindruckenden Farbänderung von gelösten Molekülen bei Variation des Lösungsmittels beruht und schon sehr lange bekannt ist. [1] Das einfachste Beispiel ist Iod gelöst in Ethanol (braun), Benzol (rot) und Tetrachlorkohlenstoff (violett). Aus physikochemischer Sicht ist die moderne Beschreibung der Solvatochromie ein typisches Beispiel dafür, dass auch wissenschaftliche Anschauungen gewissen Trends und pragmatischen Sichtweisen folgen, die historischen und theoretischen Erkenntnissen zuwiderlaufen können.
Dieser kurze Aufsatz befasst sich mit diesem Problem und versucht, die versteckten Brücken zwischen den verschiedenen Standpunkten aufzuzeigen und zum Verständnis des Themas beizutragen.
Heutzutage wird Solvatochromie ausschließlich als Effekt sich ändernder chemischer Wechselwirkungen zwischen Farbstoff und Lösungsmittel beschrieben. [2] Dies entspricht der Auffassung des Lambert-Beer'schen Gesetzes, bei dem Abweichungen ebenfalls fälschlicherweise nur auf chemische Wechselwirkungen zurückgeführt werden [3]. Diese Art von Wechselwirkungen stabilisiert oder destabilisiert entweder den Grundzustand des Farbstoffs und/oder den angeregten Zustand. Aus den sich ändernden Energieunterschieden folgen dementsprechend Verschiebungen der Banden. Diese Verschiebungen sollen es erlauben Rückschlüsse über die Wechselwirkungen zwischen Farbstoff und Lösungsmittel zu ziehen.
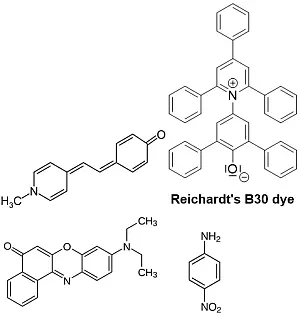
Abb. 1: Beispiele für negativ solvatochrome Farbstoffe wie
Brookers Merocyanine 4-[2-(1-Methyl-4(1H)-pyridinyliden)
ethyliden]-2,5-cyclohexadien-1-on und [2,6-diphenyl-4-
(2,4,6-triphenyl-1-pyridinium]-phenolat positiv solvato-
chromen Farbstoffe sind Nilrot (9-(Diethylamino)-5H-
benzo[a]phenoxazin-5-on) und p-Nitroanilin [4-6]
Ein charakteristisches Merkmal beider Gruppen von solvatochromen Farbstoffen ist, dass die elektronischen Grund- und Anregungszustände des Moleküls einen erheblichen Unterschied im Dipolmoment aufweisen. Diese Vorstellungen zur Solvatochromie basieren auf dem heutzutage weit verbreiteten Missverständnis, dass die Lage einer Bande in einem UV/Vis oder IR-Spektrum eine direkte Aussage zum Energieunterschied zwischen Grund- und angeregtem Zustand ermöglicht, was für Gase tatsächlich zutreffen mag.
Bei kondensierten Phasen existieren jedoch Grenzflächen, die je nachdem wie eine Messung erfolgt zu Bandenverschiebungen führen können. Des Weiteren kommt noch ein weiterer Umstand durch die Wechselwirkung von Licht und Materie hinzu, der im Folgenden noch genauer erklärt wird. Tatsächlich ergeben quantenmechanische Rechnungen, bei denen Farbstoffmoleküle mit Lösungsmittelmolekülen wechselwirken, Spektren bei denen sich solche Verschiebungen beobachten lassen.
Allerdings werden solche Rechnungen im Allgemeinen mit Molekülen im gasförmigen Zustand oder mit zu wenigen Lösungsmittelmolekülen in ihrer Umgebung durchgeführt, um den Rechenaufwand überschaubar zu halten Dabei wird ein zumindest früher allgemein bekannter, prominenter physikalischer Effekt übersehen der durch die Kondensation resultiert. Die Berücksichtigung dieses Effektes erfordert eine wesentlich größere Zahl von Lösungsmittelmolekülen, als bei theoretischen Rechnungen bislang möglich ist. Auf diesen Effekt geht der Artikel im weiteren Verlauf ein.
Solange Moleküle (oder Komplexe aus mehreren Molekülen) nämlich relativ weit voneinander entfernt sind, wie das im Gaszustand der Fall ist, entspricht die Intensität des Lichts am Ort des Moleküls der des eingestrahlten Lichtes. Dies ist für kondensierte Materie, also für Flüssigkeiten und Festkörper im Allgemeinen nicht der Fall. Wie Ende des 19. Jahrhunderts allgemein bekannt war, [7] wird ein Molekül durch einfallendes Licht polarisiert und diese Polarisation wirkt sich merklich auf die benachbarten Moleküle aus, wenn diese sich, wie in Flüssigkeiten und Festkörpern, in der unmittelbaren Nachbarschaft befinden.
Dementsprechend werden auch diese polarisiert und die entstehende Polarisation beeinflusst auch wieder das ursprüngliche Molekül. Als Folge ist die Gesamtpolarisation nicht länger direkt proportional zur Anzahl der Moleküle, sondern der Zusammenhang wird nichtlinear. Insgesamt werden die elektrische Feldstärke und damit auch die Lichtintensität am Ort eines Moleküls größer, auch wenn dies paradox erscheint. Dieser Effekt (im Englischen "Local Field Effect" genannt) wird im einfachsten Fall durch die Clausius-Mossotti Gleichung 1a, oder äquivalent, durch die Lorentz-Lorenz Gleichung 1b beschrieben [3,7,8]:
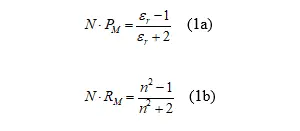
Mit:
N - molare Konzentration = Dichte/mittlere Molmasse,
PM - molare Polarisation cm3/mol,
RM - molare Refraktion cm3/mol,
εr - relative Dielektrizitätskonstante,
n - Brechungsindex.
Die Größen r und n sind abhängig von der (Mess-)Frequenz des elektrischen Feldes bzw. des Lichts. Beide Gleichungen müssen deshalb frequenzabhängig betrachtet werden. Deshalb sind alle Absorptionen über den gesamten Frequenz- oder Wellenlängenbereich gekoppelt. Im Gegensatz zu chemischen Wechselwirkungen ist diese Wechselwirkung, die (auch) zur Polarisation von Molekülen führt, nur vorhanden, wenn kondensierte Materie mit Licht bestrahlt wird. Auf ihre Relevanz für die Solvatochromie gehen wir später noch genauer ein.
Seit der Entdeckung der Merocyanine im Jahr 1951 [4] und der Pyridiniumphenolatbetainfarbstoffe im Jahr 1963 [5] (Schema 1) hat sich das Gebiet der Solvatochromie stürmisch entwickelt. Diese hat sich als wichtige empirische Methode zur Messung der Polarität von reinen Lösungsmitteln, Lösungsmittelgemischen und verschiedenen makromolekularen Materialien etabliert. [9-13]
Es gibt vor allem pragmatisch-empirische Gründe, warum sie sich als elegante Methode zur Messung der Polarität von Lösungsmitteln bewährt hat. Fast immer wird nur die M-UV/Vis-Absorptionsbande am Absorptionsmaximum (λmax) analysiert.
So wird der etablierte Dimroth-Reichardt ET(30)-Parameter der Lösungsmittelpolarität nur durch seine lösungsmittelabhängige UV/Vis-Absorptionsbande λmax in nm) in Form der molaren Absorptionsenergie in kcal/mol ausgedrückt (Gl. 2).
εr(30)[kcal/mol]= 28591/(λmax [nm]) (2)
Eine Motivation, warum diese Farbstoffe zur Messung der Polarität von Lösungsmittel dienen können, war die Tatsache, dass eine systematische Korrelation der molaren Absorptionsenergie [ET(30)] von der relative Dielektrizitätskonstante εr für verschiedene Lösungsmittelklassen gefunden wurde [5] und der ET(30) Wert mit den Ergebnissen vieler lösungsmittelabhängiger Prozesse korrelierte [2].
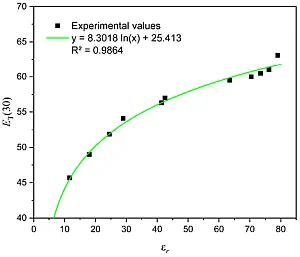
Abb. 2: Abhängigkeit des ET(30) Wertes (in kcal/mol)
von der relativen Dielektrizitätskonstante (εr) verschie-
dener OH-gruppentragender Polymere und mehrwertiger
Alkohole, Äthanol, wässrige Glukose Lösungen
sowie reinem Wassers, [19] von links nach rechts:
Polyethylenglycol, Polyvinylalcohol, Äthanol, Propylen-
glykol, Äthylenglykol, Glycerin, vier wässrige Glukose
Lösungen und Wasser. Die Daten inklusive der vier
Glukose/Wasser Lösungen (50, 30, 20 und 10 Gewichts %)
sind aufbereitet aus [9, 12-15].
Den Zusammenhang zwischen ET(30) und εr sah man als physikalische Berechtigung, daraus das Konzept der empirischen Polaritätsskalen für Reaktionsmedien zu entwickeln. Tatsächlich aber ist die statische Dielektrizitätskonstante ein Summenparameter, der proportional zur Summe der Oszillatorstärken aller Absorptionen eines Stoffes ist. Besser wäre dementsprechend eine Auftragung über die Wurzel der Differenz zwischen Molpolarisation und Molrefraktion, welche proportional dem Dipolmoment ist.
In diesem Zusammenhang sei darauf hingewiesen, dass der Brechungsindex (z.B. nD20) nicht direkt mit Dispersionswechselwirkungen in Beziehung gesetzt werden kann. Hier wird in der neueren Literatur oft Ursache und Wirkung verkehrt. So wird beispielsweise der lineare Anstieg der Brechungsindizes mit zunehmender Kettenlänge der n-Alkane durch die höhere molare Konzentration des UV-Chromophors C-H verursacht. [16] Die quantenmechanische Oszillatorstärke f des σ→σ*-Übergangs der C-H Bindung bleibt jedoch, wie auch die jeweiligen molaren Atomrefraktionen, unverändert und damit auch die Dispersionskräfte gemäß London. [17] Dieses grundlegende Missverständnis hat offenbar zu dem weit verbreiteten Irrglauben geführt, dass der Brechungsindex die Londoner Dispersionswechselwirkung des Lösungsmittels anteilmäßig widerspiegelt.
Der experimentelle Vorteil bei diesem ursprünglichen Verfahren zur Lösungsmittelpolaritätsbestimmung ist, dass man den Farbstoff nicht genau einwiegen muss, weil man nur die Position der UV/Vis Bande nutzt. Diese ist bei sehr niedrigen Farbststoffkonzentrationen in der Regel konzentrationsunabhängig vom verwendeten Farbstoff und somit ist dieses Verfahren bequem anzuwenden, vor allem wenn man experimentell unter inerten Bedingungen messen muss. Zudem kommt, dass die Reproduzierbarkeit der UV/Vis-Messung oft sehr gut ist. Die ET(30) Werte schwanken im Bereich < 1 kcal/mol. [5]
Bei der Bestimmung der empirischen Polarität von Reaktionsmedien, wurde der Zusammenhang zwischen der Bandenposition und der Bandenintensität ignoriert, weil man keine brauchbaren Zusammenhänge für Anwendungen erkannte. Diese Fehleinschätzung hatte die fatale Folge, dass man den molaren Absorptionskoeffizient oft nicht ermittelte. Da die Absorption proportional zur elektrischen Feldstärke im Quadrat, und damit zur Lichtintensität am Ort des Moleküls ist, steigt der (scheinbare) Absorptionskoeffizient eines Farbstoffes aufgrund des oben erwähnten "Local-Field-Effektes" an.
Diese beiden assoziierten Effekte, Veränderung der Intensität und Position der Farbstoffbande durch Lösungsmittel, wurden erstmals von dem Physiker August Kundt im ausgehenden 19. Jahrhunderts ausgiebig und systematisch untersucht. Kundt war nicht der erste, dem der Effekt der Farbverschiebung, zum Teil assoziiert mit Intensitätsveränderung, aufgefallen ist, aber der erste der einen gesetzmäßigen Zusammenhang dazu angeben konnte.[1] Tatsächlich wurden entsprechende Intensitätssteigerungen für ein- und demselben Farbstoff in unterschiedlichen Lösungsmitteln bis zu einem Faktor 20 beobachtet. Daneben verschiebt sich gemäß der nach Kundt benannten "Kundtschen Regel" die Bande eines Farbstoffes in einem Lösungsmittel umso stärker zu größeren Wellenlängen, je größer die Dispersion, also die Änderung des Brechungsindizes mit der Wellenlänge, des entsprechenden Lösungsmittels in dem entsprechenden Spektralbereich ist: "Hat ein farbloses Lösungsmittel ein beträchtlich größeres Brechungs und Dispersionsvermögen als ein anderes, so liegen die Absorptionsstreifen einer in den Medien gelösten Substanz bei Anwendung des ersten Mittels dem rothen Ende des Spectrums näher als bei Benutzung des zweiten." [1]
Kundt und allen seinen Kollegen, die diesen Effekt untersuchten, war bald klar, dass eine solche Rotverschiebung nicht für alle Farbstoff-Lösungsmittel Kombinationen auftritt, sondern nur in etwa 50 % der Fälle. Wie Heinrich Kayser in Band III seines damals als Referenz angesehenen Handbuchs der Spektroskopie schreibt, [18] "Es scheint nach allen diesen Angaben, dass zwar in der Kundtschen Regel ein richtiger Kern steckt, dass aber in zahllosen Fällen die nach ihr zu erwartende Wirkung durch andere Wirkungen verdeckt wird. Diese anderen Wirkungen sind im Allgemeinen unbekannt; es mögen meist chemische sein, das Entstehen von Aggregaten zwischen Lösungsmittel und Gelöstem;" und außerdem: "Jedenfalls ist der Schluss zu ziehen, dass wir uns auf die Kundtsche Regel nicht in dem Sinne verlassen können, dass wir nach ihr vorhersehen können, wie das Spectrum eines bestimmten Stoffes in einem bestimmten Lösungsmittel aussehen wird, und nur dann hätte sie practischen Werth."
Die Kundtsche Regel wurde also Anfang des 20. Jahrhunderts verworfen, weil sie die Folgen chemischer Wechselwirkungen nicht voraussagen konnte. Tatsächlich lässt sie sich aber, wie wir unlängst gezeigt haben, mit der Lorentz-Lorentz/ Clausius-Mossotti-Theorie zumindest semi-quantitativ erklären und begründen.[19] Um es nochmal explizit zu betonen, auch ohne dass sich die Lagen von Grundzustand und angeregten Zustand aufgrund von chemischen Wechselwirkung verändern, würden die Banden von Farbstoffen rotverschoben werden und erhebliche Intensitätssteigerungen zeigen, je stärker die Dispersion der Lösungsmittel im Bereich der Farbstoffbanden ist.
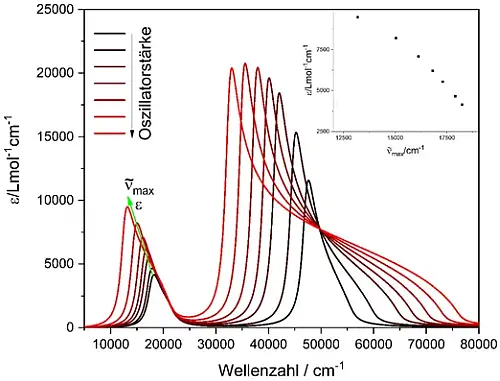
Abb. 3: UV/Vis-Spektren eines hypothetischen Farbstoffs in verschiedenen
hypothetischen Lösungsmitteln basierend auf der Lorentz-Lorenz Gleichung.
Dabei werden nur die (klassischen, konzentrationsabhängigen) Oszillator-
stärken des Lösungsmittels variiert (die Oszillatorpositionen werden nicht
verändert). In der kleinen Abbildung wird die Abhängigkeit von ε (Extinktions-
koeffizient) von der Position des Peak-Maximums des Farbstoffs gezeigt.
Bringt man etwa homologe Reihen von Lösungsmitteln zur Anwendung, so wächst deren Brechungsindex nD20 nahezu linear mit der molaren Konzentration der C-H-Bindungen (denn diese ist die "farbgebende" Gruppe im UV-Spektrum, wie bereits erwähnt).[16]
Damit steigt auch die Dispersion bei größeren Wellenlängen und Farbstoffbanden in diesen Bereichen werden rotverschoben. Folgt man weiterhin Born und Wolf, [20] so führt der von Lorentz-Lorenz und Clausius-Mossotti beschriebene Effekt zu einer Kopplung der Absorptionen von Farbstoff und Lösungsmittel (tatsächlich koppeln gemäß der Lorentz-Lorenz Gleichung alle Absorptionen, auch die im IR Bereich des Spektrums [21]).
Als Folge werden die Bandenmaxima von Farbstoff und Lösungsmittel zu größeren Wellenlängen verschoben, wenn man die klassischen, konzentrationsabhängigen Oszillatorstärken vergrößert (z.B. durch Erhöhung der Anzahl der C-H-Bindungen pro Volumeneinheit [16]), selbst wenn die Oszillatorpositionen konstant bleiben.[21] Des Weiteren führt diese Kopplung dazu, dass Konzentrationserhöhungen des Farbstoffes zu Rotverschiebungen und unproportional großen Intensitätssteigerungen führen können. Dieser Effekt ist in Abbildung 3 gezeigt.
Diesen Umstand nutzte man unbewusst bei der Bestimmung der quantitativen Zusammensetzung von Lösungsmittelgemischen mittels Solvatochromie. Demgemäß kann man aus dem gemessenen ET(30)-Wert (der Bandenverschiebung) die Zusammensetzung des Gemisches (c0 in mol/l) ermitteln (Gl. 3), [22].
Er(30)= ED (lncp /(c0+1))+ ET(0) (3)
ED und ET(0) sind empirisch ermittelte Konstanten und c0 ist die Konzentration des stärker polaren Lösungsmittels, in der Regel Wasser. Geichung 3 gilt oft nur für bestimmte Zusammensetzungsbereiche des Lösungsmittels und muss durch Kalibrierung erstellt werden. Jede individuelle Gleichung ist nur für dieses spezielle Gemisch und eine bestimmte Temperatur gültig.
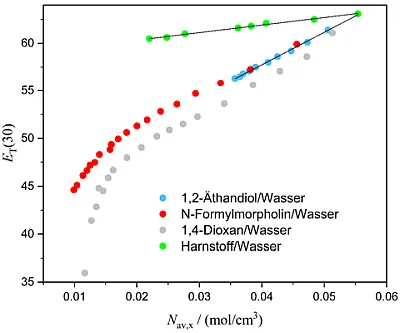
Abb. 4: Abhängigkeit des ET(30) Wertes (in kcal/mol) verschiedener
Lösungsmittelgemische bzw. wässriger Lösungen von deren mittlerer
molarer Konzentration Nav,x (mol/cm3) Harnstoff/Wasser (grün),
1,2-Äthandiol/Wasser (blau), 1,4-Dioxan/Wasser (grau) und N-Formyl-
morpholin/Wasser (rot). Die Daten wurden aus publizierten älteren
Arbeiten entnommen [23] und für diese Publikation aufgearbeitet.
Eine ungefähre Linearität zwischen ET(30) und der mittleren molaren Konzentration des Lösungsmittelgemisches findet sich vor allem für solche binären Lösungsmittelgemische in denen eine hohe Dynamik der Wasserstruktur, z.B. (1,2-Ethandiol/Wasser), mittels dielektrischer Spektroskopie gemessen wird. [24] Bleibt man im wasserreichen Teil bis ca. 80 Gew.-% Wasser, kann sehr oft Linearität zwischen ET(30) und Nav,x beobachtet werden. Abweichungen finden sich nur bei höheren Co-Lösungsmittelkonzentrationen. Dieses einfache Verfahren zur Konzentrationsbestimmung wird in der Literatur für zahlreiche Anwendungen beschrieben und wird hauptsächlich zur Bestimmung der Wasserkonzentration von wassermischbaren Lösungsmitteln verwendet. [25]
Eine sehr wichtige Erkenntnis ist, dass die UV/Vis-Position der Bande des Farbstoffs (λmax in Gl. 1) sowohl von der Konzentration als auch von der Art des Lösungsmittels abhängt. Diese Tatsache zeigt bereits, dass die gemessene Absorptionsenergie ET(30) von kolligativen, additiven und konstitutionellen Eigenschaften des Gemisches auf komplexe Weise abhängt, was eine umfassende quantitative physikalische Beschreibung erschwert. [26]
Aufgrund der leichten Handhabbarkeit von solvatochromen Farbstoffen und der sehr guten Reproduzierbarkeit der UV/Vis Messungen, hat sich die Methode der Solvatochromie auch zur Polaritätsmessung von sogenannten "Grünen Lösungsmitteln" etabliert. Dazu zählen ionische Flüssigkeiten [27], mehrkomponentige, eutektische Salzschmelzen (stark eutektische Lösungsmittel) [28] und superkritische Lösungsmittel [29]. Allerdings ist die physikalische Interpretation der Messdaten oft nicht einfach, weil Volumeneffekte und spezifische Wechselwirkung des Lösemittels kooperativ auf die solvatochrome Sonde wirken. Im Wesentlichen werden Vergleiche zwischen den verschiedenen Lösungsmittelklassen angestellt, um eine allgemeine Klassifizierung vorzunehmen und Zusammenhänge mit physikalischen Messgrößen wie dem Brechungsindex, der Dielektrizitätskonstante, Dichte oder Viskosität zu suchen Es werden Bruttoeffekte ermittelt, aus denen sich Korrelationen mit anderen physikalischen Messdaten wie Gleichgewichtskonstanten oder Reaktionsgeschwindigkeiten ableiten lassen.
Solvatochrome Farbstoffe wie der Reichardt-Farbstoff haben sich bei der Charakterisierung von anorganischen oxidischen Partikeln, synthetischen Polymeren, Polysacchariden, Cellulosederivaten und Hybridmaterialien bewährt. [9-12] Für diese Methode der Polymercharakterisierung wird zuweilen der alternative Begriff Perichromismus verwendet, um eine Abgrenzung zur Lösungschemie zu zeigen. [11] Daneben gibt es je nach Untersuchungsgegenstand, für den der solvatochrome Farbstoff verwendet wird, noch andere Begriffe wie Halochromismus, Piezochromismus, Sorptiochromismus oder Thermochromismus [30], deren umfassende Erklärung jedoch zu weit führen würde. Die jeweilige optische Eigenschaft des Moleküls beruht auf der reversiblen Farbänderung durch äußere Stimulationen. Die molekulare Struktur wird dabei nicht verändert.
Belastbare Korrelationen der Absorptionsenergie von der Polarität, über einen weiten Bereich im Sinne der statischen Dielektrizitätskonstante (Benzol εr = 2.27, Wasser εr = 78), was aber nur begrenzt sinnvoll ist (s.o.), beobachtet man bei Pyridiniumphenolatbetainen wie B30, aber nur im begrenzten Umfang bei Merocyaninen, welche oft eine inverse Solvatochromie aufweisen.[31] Inverse Solvatochromie heißt, dass bei unpolaren Lösungsmitteln ein ähnlicher hypsochromer Effekt wie bei stark polaren beobachtet wird. Damit ergibt sich keine systematische Korrelation zwischen der Absorptionsenergie, dem Absorptionskoeffizient oder der εr über einen größeren Polaritätsbereich bei vielen Merocyanin-Derivaten. Inwieweit dabei Effekte des Lichteinflusses eine Rolle spielen, ist völlig unklar.
Generell ist festzuhalten, dass Bandenverschiebungen von Farbstoffen in Lösungsmitteln nicht ausschließlich mit Änderungen chemischer Wechselwirkungen erklärt werden können. Um letztere, auch im Dunklen bestehend bleibende Effekte bestimmen zu können, müssten zuallererst Veränderungen die durch die Bestrahlung mit Licht entstehen, ab-separiert werden - gewissermaßen haben so gesehen Farbstoffe in einem Lösungsmittel im Dunklen eine andere Farbe als im Hellen. Erst dann wäre es möglich die verbleibenden Änderungen in den Spektren mit chemischen Wechselwirkungen in Beziehung zu setzen. Es bleibt zu hoffen, dass zukünftige Arbeiten sich darum bemühen beide Effekte heranzuziehen um ein größeres Verständnis der Solvatochromie zu erlangen und diesen faszinierenden und vielfältigen Effekt entsprechend seiner Bedeutung auch umfassend praktisch anwenden zu können.
Referenzen
- Kundt, Ueber den Einfluss des Lösungsmittels auf die Absorptionsspectra gelöster absorbierender Medien, Annalen der Physik, 240 (1878) 34-54.
- Reichardt, T. Welton, in Solvents and Solvent Effects in Organic Chemistry, 4th Edition, Wiley-VCH, Weinheim, 2010.
- T.G. Mayerhöfer, S. Pahlow, J. Popp, The Bouguer-Beer-Lambert Law: Shining Light on the Obscure, ChemPhysChem, 21 (2020) 2029-2046.
- L. G. S. Brooker, G. H. Keyes, R. H. Sprague, R. H. VanDyke, E. VanLare, G. VanZandt, F. L. White, H. W. J. Cressman, S. G. Dent, Color and Constitution. X.1 Absorption of the Merocyanines, J. Am. Chem. Soc. 53 (1951) 5332-5350.
- K. Dimroth, C. Reichardt, T. Siepmann, F. Bohlmann, Über Pyridinium-N-phenol-betaine und ihre Verwendung zur Charakterisierung der Polarität von Lösungsmitteln; Liebigs Ann. Chem. 661 (1963) 1-37.
- Reichardt, Solvatochromic Dyes as Solvent Polarity Indicators, Chem. Rev. 94 (1994) 2319-2358.
- H.A. Lorentz, Ueber die Beziehung zwischen der Fortpflanzungsgeschwindigkeit des Lichtes und der Körperdichte, Annalen der Physik, 245 (1880) 641-665.
- H. Kragh, The Lorenz-Lorentz Formula: Origin and Early History, Substantia, 2 (2018) 7-18.
- S. Spange, E. Vilsmeier, K. Fischer, A. Reuter, S. Prause, Y. Zimmermann, C. Schmidt, Empirical Polarity Parameters for Various Macromolecular Materials. Macromol. Rapid Commun. 21 (2000, 643-659. - Feature Article (Review)
- S. Spange, E. Vilsmeier, Y. Zimmermann, Probing the Surface Polarity of Various Silicas and Other Moderately Strong Solid Acids by Means of Different Genuine Solvatochromic Dyes, J. Phys. Chem. B 104 (2000) 6417-6428.
- L. C. Fidale, T. Heinze, O. A. El Seoud, Perichromism: A powerful tool for probing the properties of cellulose and its derivatives, Carbohydrate Polymers 93 (2013) 129-134.
- S. Mehrotra, A. Kumbharkhane, A. Chaudhari, Structural and Dynamic Characterization Using Spectroscopic Methods (chapter 8), Binary Polar Liquids (2017) 382-402.
- S. Spange, D. Keutel, Untersuchungen zur Polarität wäßriger Harnstoffund ZuckerLösungen mit der Methode der vergleichenden Solvatochromie, Liebigs Ann. (1993) 981-985.
- Dielektrische Eigenschaften verschiedener Kunststoffe nach DIN 53483, K. Biederbick, Kunststoffe, Vogel Verlag, Würzburg, 1970.
- V. Deshmukh, R. Ghongade, Measurement of dielectric properties of aqueous glucose using planar ring resonator, MicroCom (2016).
- T.G. Mayerhöfer, S. Spange, Understanding Refractive Index Changes in Homologous Series of Unbranched Organic Compounds Based on Beer's Law, Chemphyschem, 24 (2023) e202300430.
- F. London, Zur Theorie und Systematik der Molekularkräfte, Zeitschrift für Physik, 63 (1930) 245-279.
- H. Kayser, Handbuch der Spektroskopie, Vol. 3, Verlag von S. Hirzel, 1905.
- S. Spange, T.G. Mayerhöfer, The Negative Solvatochromism of Reichardt's Dye B30 - A Complementary Study, ChemPhysChem, 23 (2022) e202200100.
- M. Born, E. Wolf, A.B. Bhatia, Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, Cambridge University Press, 1999.
- T.G. Mayerhöfer, Wave Optics in Infrared Spectroscopy - Theory, Simulation and Modelling, Elsevier, 2024.
- H. Langhals, Polarity of binary liquid mixtures, Angew. Chem. 94 (1982) 739-749; Angew. Chem. Int. Ed. Engl. 1982, 21, 724-733..
- S. Spange, Polarity of organic solvent/water mixtures measured with Reichardt`s B30 and related solvatochromic probes - a critical review, Liquids (2023) submitted (may accepted).
- P. Petong, R. Pottel, U. Kaatze, Water-Ethanol Mixtures at Different Compositions and Temperatures. A Dieletric Relaxation Stud, J. Phys. Chem. A 104 (2000) 7420 -7428..
- F. Mark D. Vitha, Determining the Percent Water in Organic Solvents Using the Zwitterionic Dimroth-Reichardt Betaine ET-30 Dye. An Industrially Relevant Application of a Previously Published Laboratory Experiment, J. Chem. Educ. 78 (2001) 370.
- W. P. Jensen, Does Chemistry Have a Logical Structure? J. Chem. Educ. 75 (1998) 679-687.
- P. G. Jessop, D. A. Jessop, a D. Fua, L. Phana; Solvatochromic parameters for solvents of interest in green chemistry, Green Chem. 14 (2012) 1245-1259.
- Y. Marcus, Deep Eutectic Solvents, Springer Nature Switzerland AG (2019) ISBN 978-3-030-00607-5 ISBN 978-3-030-00608-2 (eBook)
- Y. Marcus, Solvatochromic probes in supercritical fluids, J. Phys. Org. Chem. 18 (2005) 373-384.
- C. Reichardt, Pyridinium-N-phenolate betaine dyes as empirical indicators of solvent polarity: Some new findings, Pure Appl. Chem., 80 (2008) 1415-1432
- C.E.A. de Mela, M. Domnguez, M. C. Rezende, V. G. Machado, Solvatochromism of dyes inspired in Effenberger's probe, Dyes Pigm. 184 (2021) 108757.
