04/04/2024
Assessment of the Feasibility of 2- and 3-Layer Measurements by Means of LFA
Fabia Beckstein , NETZSCH Gerätebau GmbH
Introduction
Determination of the thermal conductivity of multi-layer samples is a challenge not only for the measuring technology, but also for the operator. The Proteus® LFA soft- ware offers the possibility of measuring 2- and 3-layer samples. The analysis is carried out according to Hartmann [1] up to Proteus®7.03 and based on Maillet [2] and Baba [3] for Proteus® 7.1 upwards.
For successful measurements and reliable results, however, some prerequisites are necessary. The following questions must be answered prior to the actual measurements:
Which Paramaters Shall Be Determined in the 2-/3-Layer Measurement?
During a 2-layer measurement, the thermal diffusivity, au, and thermal conductivity, λu, of an unknown layer can be determined; see figure 1. The other layer (=substrate) must be known. It is important to note that the result for the unknown layer must always include any existing contact resistance, Rc, between the layers. It is therefore not unusual for the result from a 2-layer measurement to not correspond to the thermal conductivity of the pure material.
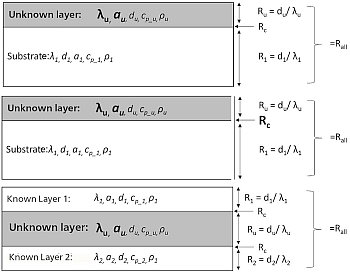
- Fig.1: Diagram of a 2-layer sample for determination of the
thermal diffusivity and thermal conductivity of the unknown layer.
Fig.2: Diagram of a 2-layer sample for determination of the
contact resistance between two layers.
Fig.3: Diagram of a 3-layer sample for determination of the
thermal diffusivity and thermal conductivity of the unknown layer.
Italics: Values must be known prior to the measurement;
Bold and large: Values are not known and are to be determined.
During a 3-layer measurement, the thermal diffusivity and thermal conductivity of one layer can be determined; see figure 3. Here, too, the result includes any contact resistance that may be present. In this measurement, it is not possible to determine the contact resistances between the layers.
Which Properties of the Layers Must Be Known?
For determination of the thermal diffusivity of an unknown layer in both 2- and 3-layer measurements, it is necessary to know the specific heat capacity, cp_u, the density, ρu and the thickness, du, of this layer. The thermal conductivity can then be calculated from this data. The thermal diffusivity, ai, the specific heat capacity, cp_i, the density, ρi, and thickness, di, of the unknown layer(s) must also be known. If the contact resistance between two layers shall be determined, the thermal diffusivity as well as the specific heat capacity, density and thickness of all layers are required.
Which Are the Requirements of the Layers?
All layers must be plane-parallel and homogeneous. The ideal thickness of the layers depends on their thermal resistance, R, compared to the total resistance, Rall.
In the following, the possibilities and limits of this method will be shown by measuring ideal samples (Pyroceram 9606, pure copper and PE). The main focus is on assessing the feasibility of multi-layer measurements and then on the interpretation and plausibility of the results.
1.) Thermal Resistance of the Unknown Layer, Ru
2- and 3-layer measurements were carried out on 1-layer reference materials. The contact resistance does not actually exist. The results of the 2- and 3-layer analyses must therefore provide the same measured value as the measurement on the reference material as a 1-layer sample. For these tests, the two reference materials, Pyroceram 9606 (Ø12.7 mm; thickness: 2.51 mm) and pure copper (Ø 12.7 mm; thickness: 2.46 mm) were used. These reference materials were selected due to their very different thermal diffusivities: Copper (at 25°C) ~ 117 mm²/s [4], Pyroceram 9606 (at 25°C) ~ 1.926 mm²/s [5].
Figures 4 and 5 show the deviation of the 2- and 3-layer measurements on Pyroceram 9606 and copper from the measurement result for the same samples as a 1-layer measurement. The x-axis gives the ratio of the thermal resistance of the unknown layer to the thermal resistance of the known layer(s). The error bars reflect the standard deviation of five individual measurements.
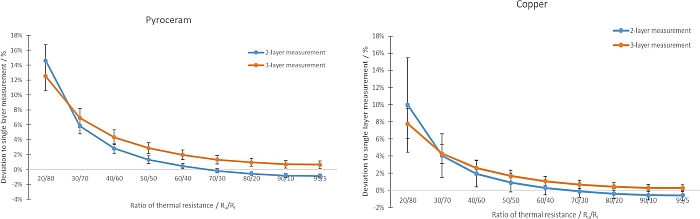
Fig.4: Deviation of the 2- and 3-layer measurement from the 1-layer measurement on Pyroceram 9606 as a function of the relationship of the thermal resistances of the unknown and known layer(s)
Fig.5: Deviation of the 2- and 3-layer measurement from the 1-layer measurement on copper, as a function of the relationship of the thermal resistances of the unknown and known layer(s)
2.) Thickness of the Individual Layers
Another basic requirement for accurate results is the precise determination of the thickness of the individual layers. An error in thickness can occur in multilayer samples due to insufficiently accurate thickness determination, non-planar parallelism or high surface roughness. A thickness error in LFA measurements must always be evaluated critically. The thickness is included in the measurement as a squared value [6]:
![]()
3.) Interpretation of the Measurement Results and Signals
Under 1), ideal samples were investigated where no contact resistance exists. However, this is not always the case with real samples. Depending on how two layers are connected together, the contact resistance is more or less distinct. For material-fit compounds (e.g., welded joints), the contact resistance is usually lower than for form-fit compounds (e.g., clamps). 2-layer and 3-layer analyses using LFA only work if the contact resistance is sufficiently low compared to the layer to be examined. This can be checked with a measurement at room temperature and agreement of the measurement signal with the mathematical fit. A polyethylene (PE) sample, consisting of two 2-mm-thick individual layers, and a Pyroceram 9606 sample, also consisting of two 2-mm-thick individual layers, were analyzed. The measurements were evaluated in three ways: Calculation of the thermal diffusivity as a 1-layer sample (incl. thermal resistance), calculation of the thermal diffusivity of an unknown layer (incl. contact resistance) and calculation of the contact resistance between two known layers.
Figure 6 summarizes the measurement signals and the result for Pyroceram 9606 and PE. The blue curves represent the detector curve recorded, and the red line, the mathematical fit (model). Good agreement between the detector curve and the mathematical fit is a basic require- ment for meaningful results.
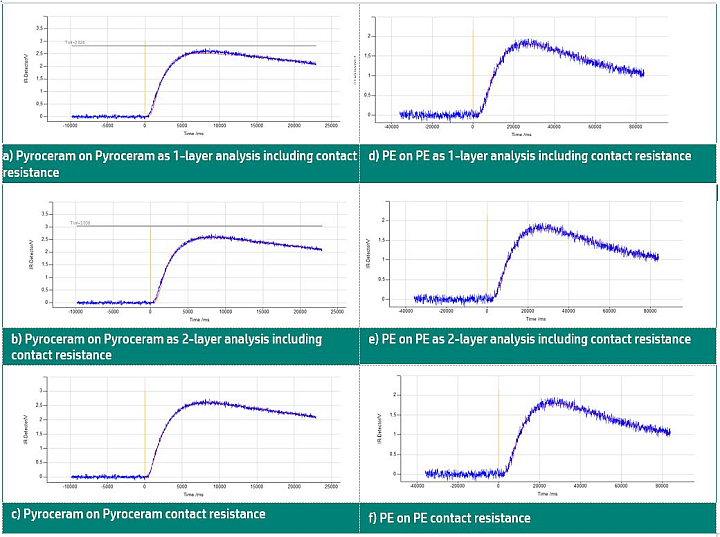
Fig.6: Detector curves and mathematical fit of Pyroceram/Pyroceram and PE/PE samples under different evaluation conditions
For the measurements of Pyroceram on Pyroceram, evaluated as a 1-layer (total thickness: 4: mm), the existing contact resistance is shown by the poor agreement of the mathematical fit with the measured signal (figure 6(a)). The measurement result is therefore subject to high error (see results in table 1). For the 2-layer analysis, the fit also does not quite agree with the detector signal.
The result (single, 2-mm-thick Pyroceram layer; figure 6(b)) now includes the existing contact resistance; this is, however, too dominant. The calculated thermal diffusivity is reduced by the contact resistance. For calculation of the contact resistance, the fit is significantly better (figure 6(c)).
The measured signals for PE on PE, on the other hand, always show good agreement (see figures 6(d), (e), (f)). Although the existing contact resistance still has influence here (see table of measurement results), it is not dominating.
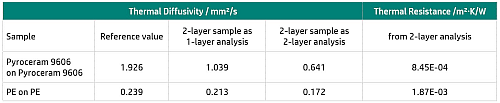
Tab.1: Analysis results for Pyroceram 9606 on Pyroceram 9606 and PE on PE
Summary
The feasibility of a multilayer analysis can be estimated by limiting the thermal resistance of the unknown layer (R > 30 % Rall). However, due to the existing and unknown contact resistances, a final statement on the feasibility of a multilayer analysis can only be made by actually measuring and interpreting the measurement signals.
(Status: up to software 8.0.3)
Abbreviation listing
Thermal diffusivity of the unknown layer: au
Thermal conductivity of the unknown layer: λu
Contact resistance: Rc
Specific heat capacity of the unknown layer: cp_u
Density of the unknown layer: ρu
Thickness of the unknown layer: du
Thermal diffusivity of the known layer(s): a1, 2
Specific heat capacity of the known layer(s): cp_1, 2
Density of the known layer(s): ρ1, 2
Thickness of the known layer(s): d1, 2
i = 1 for 2-layer measurement
i = 1 or 2 for 3-layer measurement
Thermal resistance of the unknown layer: Ru
Thermal resistance of the known layer: R1, 2
Total thermal resistance: Rall
Half time: t1/2
Literature
- J. Hartmann, O. Nilsson, J. Fricke: Thermal Diffusivity measurements on two- and three-layered systems using laser-flash method; Report ZAE 2 - 0593 - 1 (1993)
- D. Maillet, S. Andre, J.-C. Batsale, A. Degiovanni: Thermal Quadrupoles, Wiley, (2000)
- T. Baba: Analysis of One-Dimensional Heat Diffusion after Light Pulse Heating by the Response Function, Jpn. J. Appl. Phys., 48 (2009)
- Y.S. Touloukian: Thermophysical Properties of Matter - Volume 10 - Part 1 - Thermal Diffusivity
- D. Salmon, G. Roebben, A. Lamberty, R. Brandt: Certification of thermal conductivity and thermal diffusivity up to 1025 K of a glass-ceramic reference material BCR-724; Report EUR 21764 EN (2007)
- W.J. Parker, R.J. Jenkins, C.P. Butler, G.L. Abbott: Flash Method of Determining Thermal Diffusivity, Heat Capacity, and Thermal Conductivity; Journal of Applied Physics 32 (9): 1679-1684 (1961)
